My common app and links to each of my applications.
read more- Spreadsheet with Overview
- Cornell
- NYU
- UChicago
- Columbia
- Stanford
- UNC
- Princeton
- Berkeley
- MIT
- Harvard
- Duke
- Carnegie Mellon
- Yale
- General Notes
- Mensa Scholarship
Common App Essay
“It is a miracle that curiosity survives formal education.” - Albert Einstein. By the beginning of my sophomore year in high school, I had become intensely dissatisfied with the rote, mundane methodologies of conventional education. I was tired of giving priority to the topics on which I was going to be tested. I was unfulfilled by my unquestioning acceptance of knowledge. Ultimately, I was afraid of becoming just another cog in the machine. I decided I was going to learn my own way. This personal reformation was the result of questioning the personal value of receiving a good grade. I realized that I had been aspiring to meet someone else’s standards and ignoring what was truly important: my learning. A more accurate way to gauge personal progress was through introspection. When I finally began to question my own progress, I discovered gaps in my understanding covered by a carefully placed film of facts. This discovery led me to my new and current goal: to fill those gaps with well-founded understanding and to ensure that no more form as I continue my formal education. In the interest of creating and maintaining a concrete foundation of understanding, I now seek a visual and intuitive understanding of rules and concepts. I glean far more by pursuing this understanding independently than by simply learning and accepting the common proof or explanation. My results and methods are personal and thus most in tune with the way I think and reason. They are in the words I best understand: my own. This personalized understanding sometimes allows me to provide the unconventional outlook necessary to solve a problem simply whose solution would be more complex with the mainstream approach. In retrospect, the work I am the most proud of and that I have found the most enjoyable was the work I completed in the pursuit of this personalized understanding. I know this work is unique and my understanding is profound. It’s not the same essay that the past five generations have written, nor is it just another annual class project. It's the work that was formulated, executed, and completed by only me. It has my personal element instilled in it, my cognitive fingerprint.
Reviewed Independent Project List (Additional Information Section)
The following are activities that I could not report in the “Activities” section due to space restrictions: Over the course of 6 years I took weekly piano lessons. The lessons included music theory and concentrated on jazz piano. I participated in several recitals. For my 9th and 10th grade summers I was employed as a camp counselor at the University of North Carolina Farm Camp. I was responsible for the facilitation of the camp activities of children ages 6 through 9. College Courses: In the Spring of my Junior year, I took a one-semester course titled "Major Concepts in Biology" at the University of North Carolina at Greensboro. I received an A in the course. UNC-Greensboro will be sending you an official transcript. In this Fall of my Senior year, I am taking two courses at the University of North Carolina at Chapel Hill. The courses are Math 232, "Calculus of Functions of One Variable", and Chemistry 101, "General Descriptive Chemistry". In the Spring of my Senior year, I will be taking Math 233, “Multivariable Calculus”, and Math 381, “Discrete Mathematics”. Unfortunately, a transcript will not be available in time for my Early Decision/Action applications, but will be available in time for my Regular Decision applications. This past summer, I interned at a Physical Chemistry lab at the University of North Carolina at Chapel Hill. The graduate students I worked with were studying semiconductor nanostructures using ultrafast spectroscopy with the goal of developing materials for efficient solar fuels production. The results of our research have been accepted for publication in "The Journal of Physical Chemistry". I am a co-author on the paper. The complete paper is now available at http://pubs.acs.org/doi/abs/10.1021/jp207830h . The following summaries of some of my larger scale independent projects will show how I have supplemented by formal education over the past few years. Analyzing the Network of Facebook I wrote a program that takes the friends of any given Facebook user and stores the list in a database and subsequently takes the friends of each of their friends (eliminating mutual friends) in order to discover the rate of growth of the network after starting from a given node. The objective was to compare rate of growth to the postulated 6 degrees of separation between any two individuals. Additionally, I generated formulas to compare the interconnectedness of a node and its connections, of a given section of a network, and of an entire network. Analyzing the Network of Words Similar to the Facebook network analysis program, I wrote a program that uses words listed as synonyms in a common dictionary resource to form a network and then calculate the number of words that can be reached from any given word through its synonyms, and its synonyms' synonyms, etc. Accidental discovery of the normal distribution curve In an attempt to understand the nature of permutations, I found all the permutations of a four-digit binary number (0001,0010, etc). I noticed that if I tallied the number of times a given number of 1’s appeared for each permutation, I would get a much higher occurrence of two 1’s than four or zero 1’s. I also found that if I graphed these tallies, the results had a bell shape. I subsequently wrote a program that does this tallying for a much longer binary number and found similar results. I hypothesized that if I were to take the limit as the length of the permuted binary number approached infinity, I would get a perfect normal distribution curve. When I brought this hypothesis to a math teacher at my high school, he said it was valid and pointed out that I had been calculating rows of Pascal’s triangle. Poking Fun with Facebook Employing some of the same programming techniques I developed while writing my Facebook Network analysis program, I wrote a simple program that used Facebook’s “poke” functionality to poke all my friends on the site. Modeling a Dynamical System Inspired by an episode of “The Office” in which the employees watch a DVD logo bounce on a T.V. screen, I wrote a program that models the trajectory of a circle bouncing within a square. I observed the periodicity of the circle’s movement given varying starting angles and positions within the square and I hope to produce Chaotic (aperiodic) behavior by expanding this program to other shapes bouncing within an ellipse. Geometrical Representation of The Birthday Paradox Prompted by our homeroom teacher writing down student’s birthdays on the first day of my twelve grade year and observing that my birthday fell on the same day as another student’s, I decided to investigate the Birthday Paradox: a phenomenon I was familiar with but did not understand intuitively at that time. The Birthday Paradox is the observation that the probability that any two individuals in a group have the same birthday is higher than one would expect (50% chance in a group of 23 people). After some thought on how I should approach the problem, I decided to try to represent the problem geometrically. For the combinations of birthdays two people could have, I imagined a 365x365 plane in which each point was a birthday combination. I noticed that the diagonal of this square contained birthdays that fell on the same day (I also noticed that this “plane” wasn’t really a plane at all but rather a set of points that all fell on the same plane). I expanded to three people (thus, requiring three dimensions) and found, out of a cube, three planes intersecting planes contained the birthdays that fell on the same day. I eventually came to completing the far more complicated four dimensional problem. Each time, my results were consistent with the results of the preexisting convoluted equation used for this computation: The following are titles of other projects or investigations I have conducted independently: Investigation of the geometric meaning of the integral of sin(x) as it pertains to the unit circle Defining three-dimensional objects using transformations of two-dimensional shapes Animated electromagnetic field produced by two charges as one’s position varies Program that plays a probability based gambling game that dynamically improves its performance Representing Tangent, Secant, Cosecant, and other trigonometric functions as line segments on the unit circle Book introduction: The Art of Nonconformity Investigation of the rate of divergence of improper integrals Program that calculates definite integrals and uses the results to find minimums and maximums of the inputed function Investigation of the set produced by dividing a Fibonacci number by the sum of all previous terms Measuring the period of the length of Fibonacci numbers Graphing 3D electric force vectors Examination of optimal circle packing Understanding the limit definition of e and compound interest as the interest of interest Investigation of the spiral produced by the parametric binomial expansion of complex numbers Program that creates and graphs a bifurcation diagram (allowing the observation of the aperiodic behavior dynamical systems are capable of) Program that simulates the Monty Hall problem Investigation and analysis of the cognitive dissonance engendered from my transition from typing in a QWERTY keyboard layout to a Dvorak layout Investigation of 1-1/2+1/3…, later found to be the “alternating harmonic series” Investigation of the geometric relationship between prime numbers
Screenshots of Extracurriculars
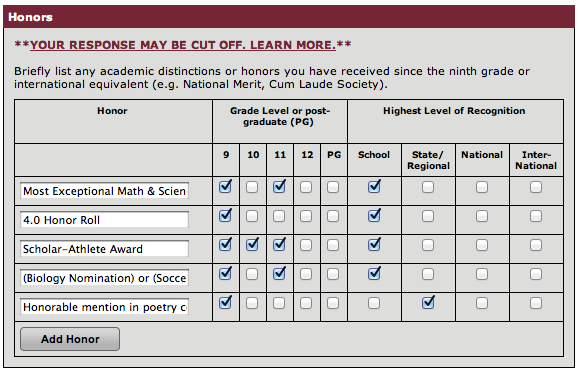
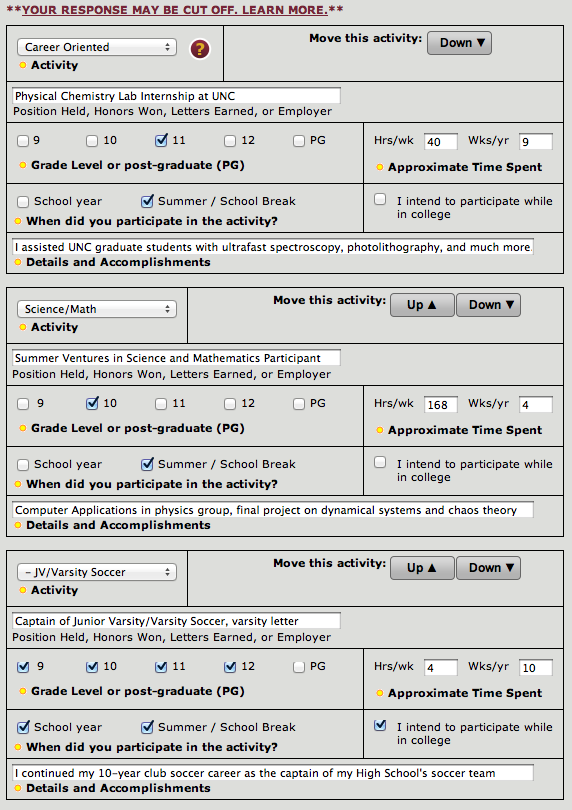
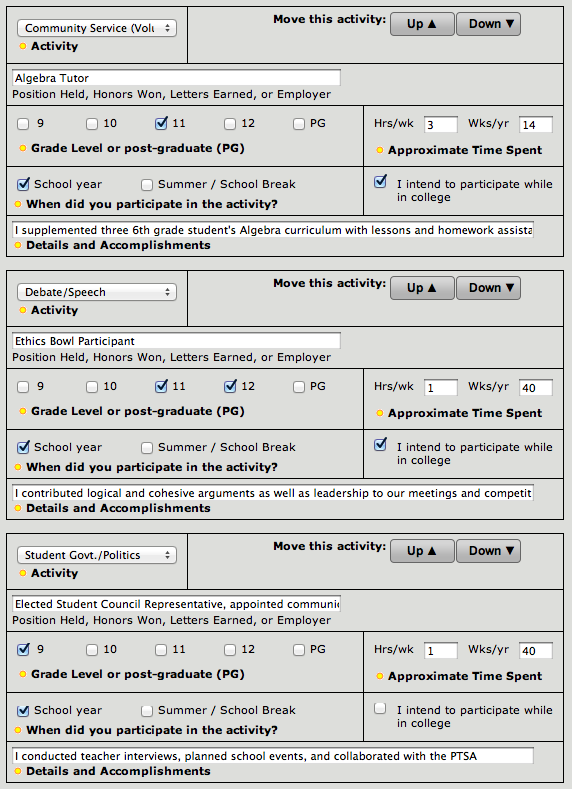
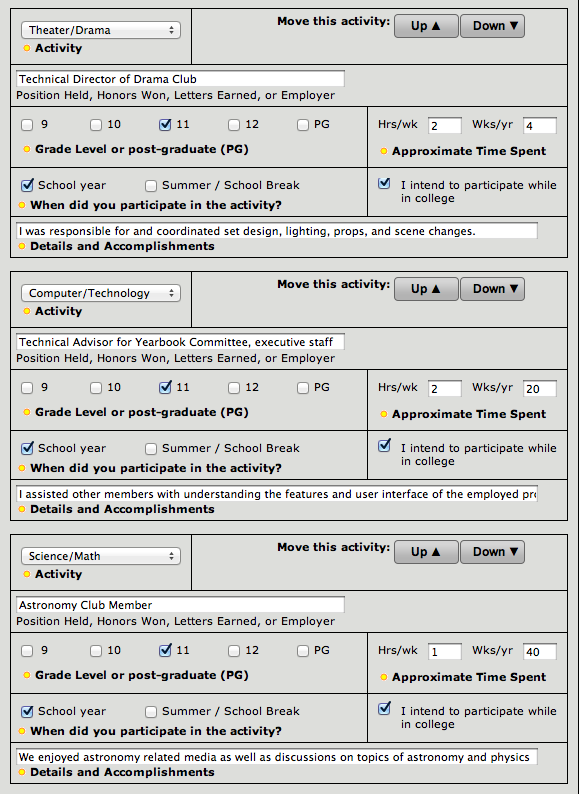
Please briefly elaborate on one of your extracurricular activities or work experiences in the space below (1000 character maximum).
During my 11th grade summer, I interned at a Physical Chemistry lab at UNC. The group of graduate students I worked with were studying semiconductor nanostructures using ultrafast spectroscopy with the goal of developing materials for efficient solar fuels production. Being the only intern on the team, I originally found keeping up with the student’s research remarkably difficult. Although, through perseverance, asking questions, and my own research I was able to not only understand their work but also contribute and eventually coauthor one of their publications. At the time, our team was concerned with observing the transfer of energy over time within a semiconducting material (Zinc-oxide). We used two beams of pulsed light originating from a laser, the first of which excited a region of the material, while the second probed the energy of the region at regular femtosecond intervals. The results of our research will be published in “The Journal of Physical Chemistry.”