It's been 8 years and I'm still not over how much of a waste of time diff eq was.
read more
linear algebra that we covered, linear independence, whether a presentation is unique,
The stuff in our homework (3.1 - 3.6)
gauss elimination will be used to do the above
equations of the second order: solutions of homogeneous
Suppose we want to integrate t^n e^(at) dt, <—Could not find this
integral of e^(at) = e^(at)/a <— this is just obvious.
nth derivative of the above <— this is just iterating the above
The start of studying:
3.1
So the basic equation is ay’’ + by’ + cy = 0, where a,b,c are constants.
We start by looking for equations of the form y=e^(rt), where we need to find r.
We know that y’=re^rt and y’’=r^2e^rt .
We can essentially rewrite the equation as ar^2 + br + c = 0. which we call the characteristic equation.
We hopefully can factor this to get (r+x)(r+y) and -x and -y are our solutions.
Remember that we are looking for equations of the form y=c_1e^(r1t)+c_2e^(r2t). Any linear combination (that is, any choices of c_1 or c_2) would constitute a solution, but a specific c_1 and c_2 are required if initial values are given.
Maybe practice this ^ one with Yang, even though it’s pretty straightforward.
3.2
L[y] = y’’ + p(t)*y’ + q(t)*y = g(t) . L is an operator.
For a function of the form L[y], with initial values, we know that 1. a solution exists, there is only one solution, and it’s defined on the entire interval.
W = | y1(t) y2(t) |
| y’1(t) y’2(t) |
= y1(t)y’2(t) - y’1(t)y2(t)
If W is not equal to 0, then the equation has a unique solution, regardless of the initial condition given.
This unique solution is given by:
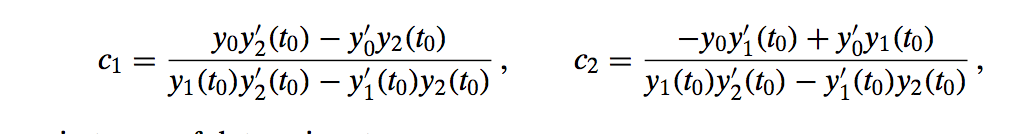If W=0, then it will have no solution that satisfies the initial conditions.
Things I need to know how to do:
Find general solution of given differential. Break up into characteristic equation, by taking coefficients. So y’’ + 5y’ + 6y = 0 goes to r^2 + 5r + 6 = 0. Then solve for r, which should give two possible values, r1 and r2. The solution is y=c1*e^(r1*t)+c2*e^(r2*t).
Find specific solution of given initial value problem. This is the same thing as above. Break it into the characteristic equation, solve for r1 and r2, to get your general solution. They’ll specify a y(0) and a y’(0), so you need to plug in t for the general solution which should get you something like c1+c2=2, and then you need to differentiate and plug in y’(0), then you should have two equations involving c1 and c2.
Use Euler’s formula to write an expression of the form a+ib. Euler’s formula is e^(it) = cos(t)+i*sin(t). So, e^(1+2i) would be equal to e*cos(2) + i * e * sin(2). Notice that we can split it up to be e^1 * e^2i, but we have to remember to multiply everything by e in the end.
Calculate the Wronskian (if nonzero) will determine if the solutions of the equation can be written as arbitrary linear combination (that is, y=c_1*y_1 + c_2*y_2). To calculate the Wronskian, we just need y1(t)y’2(t) - y’1(t)y2(t). If this is zero, we can’t write as linear combination.
Solving the differential equation when b^2 - 4ac is negative (non real roots). Remember the equation is ar^2 + br + c = 0. If the discriminant is negative, the roots are conjugate complex, which means r1 = lambda + i *mu and r2 = lambda - i *mu. Use quadratic formula and reduce down to get roots. Should be 
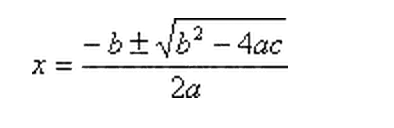. Say the solution is r1, plugin to the equation e^(r1*t), so you should end up getting one term that has no imaginary numbers, and one that does. For the one that does, you should break it up as cos + i*sin. Where the coefficient of t remains the same. So e^(3*i*t) = \cos(3t)+i*sin(3t). Once you do this, if you want to find the real solution (a non-imaginary one), TAKE THE SUM AND THE DIFFERENCE OF THE EQUATIONS, AND EACH OF THOSE SHOULD BE REAL SOLUTIONS. Once you do this, you can take out any constant multipliers (including i) and then you have your real.
Figure out solutions to differential equations where there are repeated roots, that is when b^2-4ac = 0. When this is the case, we should be getting one solution to the equation, and we just know that y_1(t) = e^(-bt/2a) and y2(t)= t*e^(-bt/2a).
For nonhomogeneous equations, that is, functions that do not have 0 on the right hand side. This solution is very guess and check. For a non homogeneous equation we have solve it by first considering it a homogeneous equation (making the right hand side = 0) and then solving it normally. Then we seek a function Y=A*y(t) that satisfies the non homogeneous equation. The actual solution is the sum of the two.
Find the inverse of a matrix. To solve this, we augment the matrix with the Identity matrix and then try to change the original matrix to the identity matrix and do all the operations we did on the original matrix also on the identity matrix.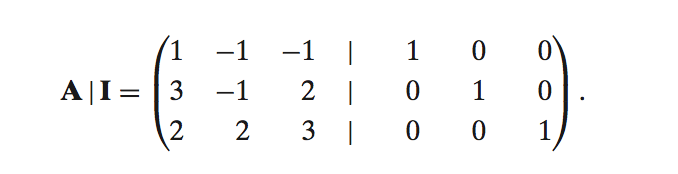 
Check linear independence. Augment the matrix with all zeros, and then do gauss elimination to try to get an entire row to be all zeros. Then try to write one term completely in terms of other two. Then try to get the equation a*c1+b*c2+c*c3 = 0. If you can do this, then it’s linearly dependent.
STILL NEED TO LOOK AT 3.6.
Good Summary for the above three problem types

Amalgam of main theorems

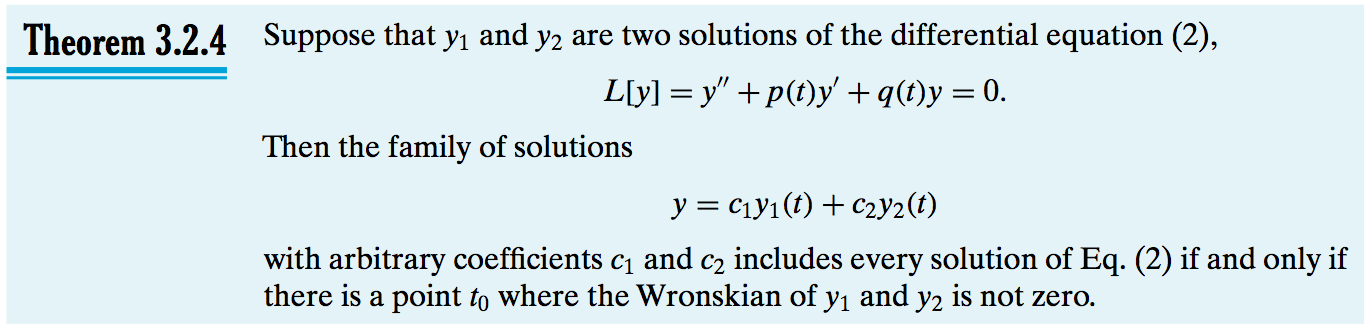
Assignments:
8/29
Sect. 2.2: 1, 2, 3, 4, 6, 8; Sect. 2.1: 13, 14, 15, 17
9/5
Sect 2.2: 31, 32; Sect 2.4: 28, 29; Sect 2.6: 7-9, 10, 12, 13
9/17
Sect 7.2: 1, 6 (a, b, c) (compute explicitly both sides)
9/29
Sect 7.3: 1, 2, 3, 4, 5, file hw1
10/3
file hw2
10/8
file hw3; Sect. 3.1: 1, 2, 3, 6, 9, 10, 13
10/22
Sect. 3.3: 1, 2-6, 7, 9, 10, 17, 18, 19
10/24
Sect 3.4: 1, 5, 6, 12, 14
10/29
Sect 3.5: 1, 3, 5, 7, 8, 10, 17, 19
10/31
Sect 3.6: 1, 2, 3, 5, 13, 15