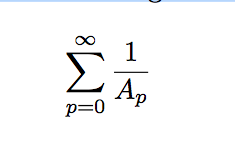read more 
Intro, prime types, mersenne 2^n -1 where n is natural. twin primes p+2, cousin, etc. 

New prime type: 2p+q=r, where p and q are consecutive. Similar to goldbach who said p+q+r = any number. 

Discovery of aidian primes. room number 385

Questions as a result: What fraction of Aidian primes have a neighboring Aidian prime? 

Does every Aidian prime have a unique p, q pair?

 If two primes are yielded from this operation, are they necessarily consecutive?

Are there infinitely many primes of this form?

What is the distribution of Aidian primes within the integers?

What if the restriction that p and q be consecutive is dropped? 

What if we consider all primes that can be written as a linear combination of another two, that is: r = np + mq where n, m are integers and p, q are consecutive primes?


 353 = 2(113)+127 and 367 = 2(127)+113. Between the primes 353 and 367 lies the prime 359.

Using a computer we found that out of the 5561 Aidian primes generated by p, q pairs taken from the first 25000 primes, all had a unique p, q pair. 

It may also be observed that the set of numbers resulting from inputs of consecutive primes p,q into 2p + q is necessarily going to be monotonically increasing, which allows us to conclude that each r = 2p + q will be possible only from a distinct choice of p, q. 

For each Aidian prime, we mark
whether one of its neighboring primes is Aidian, or if neither are Aidian.
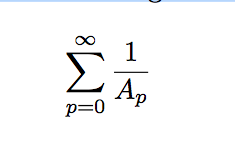
 Using a computer, we first generate a list of all Aidian primes up to a certain number (100000), then we cycle through all the Aidian primes, taking the inverse (in order to for a logarithmic fit) of the following ratio:  This suggests that the distribution of Aidian primes among the integers is ”nice”. That is, the change in their distribution between segments of the integers follows some pattern. More investigation should be conducted on this distribution. Next, we examine the distribution of primes c such that c = 2a + b where a,b be prime but not necessarily consecutive primes. We may also gain some intuition regarding their cardinality by getting a sense for whether the following series diverges: