read more
Cumulative.
Dynamic programming
Greedy algorithms
Time complexities and invariants for basic graph algorithms.
Old stuff
Hashing? perhaps for a question that uses random variables.
Will use graphs as a basis for dynamic programming or greedy algorithms.
Dynamic Programming:
Essentially, Dynamic Programming is just divide and conquer (recursion), but breaking things up in a way such that the subproblems may overlap, so that you can essentially save time by eliminating redundant calculations. You store solutions to previous subproblems, so that when you encounter them again you don’t have to recalculate.
Greedy Algorithm Property: essentially just showing that the greedy algorithm is going to do at least as well as the optimal?
A greedy algorithm would be used if there isn’t overlapping subproblems. If there are, we want to use dynamic programming. Additionally, for greedy problems, any locally optimal choice must be a globally optimal solution (so greedy problems are a subset of Dynamic Programming problems). ???
Trying to define “optimal substructure”: the proposed structure of a solution such that subproblems of that solution can be solved identically. That is, the end solution is simply a combination of subproblems (where there may be overlap in subproblems).
So thinking about two strings and trying to find the longest common subsequence, you would try to think “okay, well say we have a greatest common subsequence, what are its qualities?” essentially, you start to see that this is a nested problem, as you can look at a subsequence that’s one smaller than your GCS should be a GCS of either one less of one string, the other string, or both (depending on the end of the GCS string). This recursive solution is best summed up by this:
 
Don’t really understand the bottom-up solution. Do we need to know it?
For the binary tree problem, essentially you figure that this has optimal substructure in that when examining any given subtree, that subtree should itself be an independent, optimal solution. Of course, when unpacking, you can see that the subtrees overlap, that is, if you have tree T, and look at T.right and T.left, each of these are nested inside the combined problem.
Methods for solving Dynamic Programming problem: 1. state the end-solution 2. Show that you had to do an if statement to get to that end solution 3. This if statement should have some recursive calls in it, which are the subproblems 4. claim that subparts of this solution must be optimal themselves (that is, if the problem were these smaller subproblems, then those problems would be the solution).
Invariants for all of the graph algorithms and the run-time complexities.
Basic Graph Algorithms:
If vertex is connected, there is a path between every pair of vertices. |E| \geq |V| -1.
If |E| = |V| -1, then it’s a tree.
A forrest is a collection of trees.
Adjacency lists just stores a linked list of all vertices connected to a given vertex. So max size would be V^2.
Adjacency list requires O(V+E) storage for directed and undirected.
Adjacency is best for sparse, matrix is best for dense.

Don’t really understand the bottom-up solution. Do we need to know it?
For the binary tree problem, essentially you figure that this has optimal substructure in that when examining any given subtree, that subtree should itself be an independent, optimal solution. Of course, when unpacking, you can see that the subtrees overlap, that is, if you have tree T, and look at T.right and T.left, each of these are nested inside the combined problem.
Methods for solving Dynamic Programming problem: 1. state the end-solution 2. Show that you had to do an if statement to get to that end solution 3. This if statement should have some recursive calls in it, which are the subproblems 4. claim that subparts of this solution must be optimal themselves (that is, if the problem were these smaller subproblems, then those problems would be the solution).
Invariants for all of the graph algorithms and the run-time complexities.
Basic Graph Algorithms:
If vertex is connected, there is a path between every pair of vertices. |E| \geq |V| -1.
If |E| = |V| -1, then it’s a tree.
A forrest is a collection of trees.
Adjacency lists just stores a linked list of all vertices connected to a given vertex. So max size would be V^2.
Adjacency list requires O(V+E) storage for directed and undirected.
Adjacency is best for sparse, matrix is best for dense.
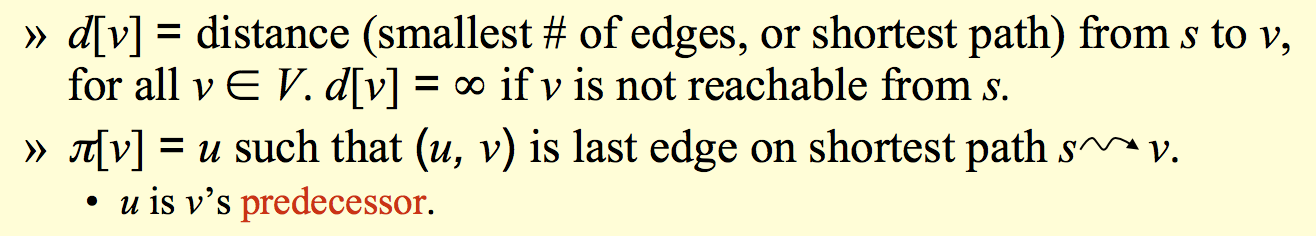 

Breath first:
Run-time: O(V+E)
Essentially, you start at some position and go uniformly out, in a layered fashion.
Invariant: Queue contains all (discovered) adjacent vertices in discovered/increasing distance order from source


Breath first:
Run-time: O(V+E)
Essentially, you start at some position and go uniformly out, in a layered fashion.
Invariant: Queue contains all (discovered) adjacent vertices in discovered/increasing distance order from source
 

Depth first:
Run-time: O(2V+E)
Invariant: Vertex’s discovered time is > that of all previously discovered vertices and finishing time> all finishing times of vertices adjacent.


Depth first:
Run-time: O(2V+E)
Invariant: Vertex’s discovered time is > that of all previously discovered vertices and finishing time> all finishing times of vertices adjacent.
 Don’t really understand the bottom-up solution. Do we need to know it? For the binary tree problem, essentially you figure that this has optimal substructure in that when examining any given subtree, that subtree should itself be an independent, optimal solution. Of course, when unpacking, you can see that the subtrees overlap, that is, if you have tree T, and look at T.right and T.left, each of these are nested inside the combined problem. Methods for solving Dynamic Programming problem: 1. state the end-solution 2. Show that you had to do an if statement to get to that end solution 3. This if statement should have some recursive calls in it, which are the subproblems 4. claim that subparts of this solution must be optimal themselves (that is, if the problem were these smaller subproblems, then those problems would be the solution). Invariants for all of the graph algorithms and the run-time complexities. Basic Graph Algorithms: If vertex is connected, there is a path between every pair of vertices. |E| \geq |V| -1. If |E| = |V| -1, then it’s a tree. A forrest is a collection of trees. Adjacency lists just stores a linked list of all vertices connected to a given vertex. So max size would be V^2. Adjacency list requires O(V+E) storage for directed and undirected. Adjacency is best for sparse, matrix is best for dense.
  Breath first: Run-time: O(V+E) Essentially, you start at some position and go uniformly out, in a layered fashion. Invariant: Queue contains all (discovered) adjacent vertices in discovered/increasing distance order from source
  Depth first: Run-time: O(2V+E) Invariant: Vertex’s discovered time is > that of all previously discovered vertices and finishing time> all finishing times of vertices adjacent.