read more
Final prep for Comp 455
After midterm 2 condensed:
Need to better understand the Delta.
 Hierarchy between languages (subsets):
Finite < Regular < Context Free < Decidable < Partially Decidable
Chomsky normal form: a given transition (e.g. A->BC) must at most result in two non-terminals. So you can’t have A->BCD. Unpacking string n takes 2n-1 steps in this form.
PDA determinism: given any config, you can only go to one other config.
Turing machine: decidable if halts on all inputs (accepting those in L and rejecting those not), partially decidable if halts on accepted inputs and either halts or loops on rejected inputs. Output is what’s left on the tap after halting. Equivalent to general grammars.
General grammar equiv. to context sensitive. They mean that a transition for a character may depend on what’s around it. uAv -> uwv (u, v, don’t change but A going to w requires those surrounding characters).
Universal Turing Machine: this is a turing machine that can simulate other turing machines (essentially, a modern computer that can run multiple programs). It takes two inputs, T and x and it runs T on x. If it halts, that means T halted on x. In order to pass a turing machine to a Universal Turing Machine, we have to encode the turing machine being passed. We can do that by encoding its delta function. This is the entire ((q00, a000, q10, a000), (q00, a001, q01, a011)…) business. You encode the input string using the same scheme that you used for the Turing Machine because each character in the language should be defined as an input in the Turing Machine. Passing to a Universal Turing Machine is essentially just concatenating the two encodings: encode(M)encode(x) where M is the Turing Machine and x is the input.
Halting Problem is: can you construct a Universal Turing Machine that halts on all inputs, that is, can you create a Universal Turing Machine that is decidable, that is, that can figure out if any algorithm will loop forever. The conclusion is no you can’t create such a Universal Turing Machine.
Hierarchy between languages (subsets):
Finite < Regular < Context Free < Decidable < Partially Decidable
Chomsky normal form: a given transition (e.g. A->BC) must at most result in two non-terminals. So you can’t have A->BCD. Unpacking string n takes 2n-1 steps in this form.
PDA determinism: given any config, you can only go to one other config.
Turing machine: decidable if halts on all inputs (accepting those in L and rejecting those not), partially decidable if halts on accepted inputs and either halts or loops on rejected inputs. Output is what’s left on the tap after halting. Equivalent to general grammars.
General grammar equiv. to context sensitive. They mean that a transition for a character may depend on what’s around it. uAv -> uwv (u, v, don’t change but A going to w requires those surrounding characters).
Universal Turing Machine: this is a turing machine that can simulate other turing machines (essentially, a modern computer that can run multiple programs). It takes two inputs, T and x and it runs T on x. If it halts, that means T halted on x. In order to pass a turing machine to a Universal Turing Machine, we have to encode the turing machine being passed. We can do that by encoding its delta function. This is the entire ((q00, a000, q10, a000), (q00, a001, q01, a011)…) business. You encode the input string using the same scheme that you used for the Turing Machine because each character in the language should be defined as an input in the Turing Machine. Passing to a Universal Turing Machine is essentially just concatenating the two encodings: encode(M)encode(x) where M is the Turing Machine and x is the input.
Halting Problem is: can you construct a Universal Turing Machine that halts on all inputs, that is, can you create a Universal Turing Machine that is decidable, that is, that can figure out if any algorithm will loop forever. The conclusion is no you can’t create such a Universal Turing Machine.
 QUICK AND DIRTY FACTS:
Regular are closed under: L1 U L2 (union), L1L2 (concatenation), L1* (kleene star), L1 intersect L2 (intersection).
Context free is closed under: union, concatenation, klene star, union with regular, intersection with regular.
Iff has finitely many equivalence classes, then L is a regular language.
Equivalence with respect to language: for each char in L, next to it what you can add to the end of it (as a set) and still get something into L. Then read off what’s equivalent.
Things Turing Machines can recognize (therefore, things that have a General grammar):
a^n b^n c^n.
Remember, turing machines have a state at any given input as well. We can write this as:
QUICK AND DIRTY FACTS:
Regular are closed under: L1 U L2 (union), L1L2 (concatenation), L1* (kleene star), L1 intersect L2 (intersection).
Context free is closed under: union, concatenation, klene star, union with regular, intersection with regular.
Iff has finitely many equivalence classes, then L is a regular language.
Equivalence with respect to language: for each char in L, next to it what you can add to the end of it (as a set) and still get something into L. Then read off what’s equivalent.
Things Turing Machines can recognize (therefore, things that have a General grammar):
a^n b^n c^n.
Remember, turing machines have a state at any given input as well. We can write this as:
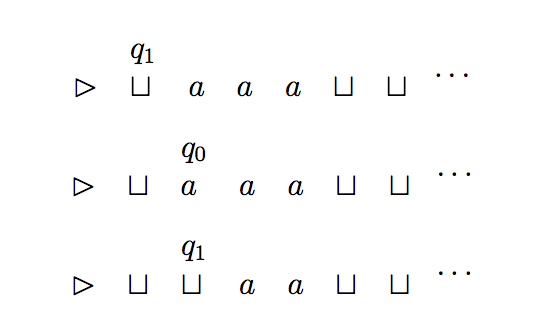
 Next: UNDERSTAND THE GENERAL METHOD TO SHOW UNDECIDABILITY. (http://www.cs.unc.edu/~plaisted/comp455/slides/unsolv5.4.pdf)
Pumping Lemma: This is to say: If you can choose a string in L of arbitrary length (any n choice) such that if you were to split it up and copy the middle portion a certain number of times, the resulting string would NOT be in L, then you have won and shown that the language is not regular. If the opponent wins, that doesn’t necessarily mean the language is regular. You can’t use the game to show regularity, just show irregularity.
Stuff after midterm 2:
Chomsky normal form (changing the unpacking steps so that there are most one nonterminal to two nonterminals essentially), which is good because then if you’re doing an exhaustive attempt to generate a string each unpacking for string length n takes 2n-1 steps.
Determinism in push down automata, is exactly what you’d expect. At any given configuration, is there more than one transition that you can take to get to the next one? If there isn’t, then it’s deterministic.
Context free languages are closed under complementation.
Next: UNDERSTAND THE GENERAL METHOD TO SHOW UNDECIDABILITY. (http://www.cs.unc.edu/~plaisted/comp455/slides/unsolv5.4.pdf)
Pumping Lemma: This is to say: If you can choose a string in L of arbitrary length (any n choice) such that if you were to split it up and copy the middle portion a certain number of times, the resulting string would NOT be in L, then you have won and shown that the language is not regular. If the opponent wins, that doesn’t necessarily mean the language is regular. You can’t use the game to show regularity, just show irregularity.
Stuff after midterm 2:
Chomsky normal form (changing the unpacking steps so that there are most one nonterminal to two nonterminals essentially), which is good because then if you’re doing an exhaustive attempt to generate a string each unpacking for string length n takes 2n-1 steps.
Determinism in push down automata, is exactly what you’d expect. At any given configuration, is there more than one transition that you can take to get to the next one? If there isn’t, then it’s deterministic.
Context free languages are closed under complementation.
 Turing machine can recognize a^nb^nc^n
Turing machine is decidable if for all inputs, it accepts those in L and rejects those not in L. So either way it halts.
Turing machine semidecides language sigma* if it accepts all inputs in L and rejects or loops all inputs not in L. So accept is always halt but reject may not always be halt.
So all machines that are decidable are also semidecidable/partially decidable.
So turing machines can accept or reject inputs (both of which are instances of it halting) or it can just loop infinitely.
Turing machine can recognize a^nb^nc^n
Turing machine is decidable if for all inputs, it accepts those in L and rejects those not in L. So either way it halts.
Turing machine semidecides language sigma* if it accepts all inputs in L and rejects or loops all inputs not in L. So accept is always halt but reject may not always be halt.
So all machines that are decidable are also semidecidable/partially decidable.
So turing machines can accept or reject inputs (both of which are instances of it halting) or it can just loop infinitely.
 So to determine the decidability of a problem, we’re actually making a language that represents that problem and then seeing if there’s a turing machine that accepts that language.
Output of a turing machine is what’s left on the tap after halting.
Busy beaver function essentially shows that some machines will halt after a large number of steps and so you can’t say “let’s just compute first 1000 iterations and if it doesn’t halt then it’ll never halt” because some might.
One thing to know is that nondeterminism doesn’t add power, but I don’t really understand what it is. It seems like you have have multiple transitions for a given configuration and your automaton essentially (you can imagine it like this) takes all transitions possible and then it would have guessed the right one.
General grammars are more reaching and they encompass I think any of the grammars we’ve talked about. For example, context free grammars are also general grammars.
Context sensitive/specific is interesting. An example of a production that is context sensitive is uAv -> uwv. This is specific because the change of A depends on what’s around it. The cool thing is that this represents english grammar because a word has different meanings in context.
So when trying to figure out if a language is context-free, and you come up with a grammar for it, how do we know you didn’t choose a rule that is context _sensitive_? I guess our rules have to have every item in the left and ride side be different? You can’t do something like aba -> aca but cbc -> cac because that change of the middle b would depend on what is around it.
General grammars are equivalent to turing machines. They both generate context sensitive languages.
Universal turing machine takes an input T, a turing machine. It can simulate T on its own input, x. If this turing machine halts on inputs (T,x) then that means that T halted on x. We need to encode the actual turing machine as a string of symbols.
Universal turing machines are essentially modern computers, as they can execute multiple programs (each of which are their own turing machines).
So in order to encode a turing machine, we pretty much just have to encode its delta function. That is, what state it goes to and what gets read given it’s at a given state, reading a given input. (s,a,q, U) for example.
Encoding input strings is done the same way, and because every string you’ll read is going to be in the language, you just use the encoding that you got from encoding the delta function.
M reads in in encoding of T and encoding of an input to T (x) concatenated… encode(M)encode(x).
What does “recursively enumerable” mean? IT MEANS PARTIALLY DECIDABLE.
The halting problem is: “given a computer program and some input, determine whether or not the program halts/finishes executing”. That is, can a universal turing machine be constructed so that inputs are decidable? Yeah I think that’s what it says. So essentially there is no program you can write that will be able to take any algorithm and an input and decide if that algorithm halts on that input.
Delta is all turing machines that loop on the input of themselves?
Regular languages == regular grammars == deterministic finite automata
Context-free languages == context-free grammars == push down automata
Context-sensitive languages == context-sensitive grammars == linear bounded automata
Recursive languages == (no equivalent grammar) == Turing machines that always halt
Recursively enumerable == general grammars == turing machines
Helpful:
So to determine the decidability of a problem, we’re actually making a language that represents that problem and then seeing if there’s a turing machine that accepts that language.
Output of a turing machine is what’s left on the tap after halting.
Busy beaver function essentially shows that some machines will halt after a large number of steps and so you can’t say “let’s just compute first 1000 iterations and if it doesn’t halt then it’ll never halt” because some might.
One thing to know is that nondeterminism doesn’t add power, but I don’t really understand what it is. It seems like you have have multiple transitions for a given configuration and your automaton essentially (you can imagine it like this) takes all transitions possible and then it would have guessed the right one.
General grammars are more reaching and they encompass I think any of the grammars we’ve talked about. For example, context free grammars are also general grammars.
Context sensitive/specific is interesting. An example of a production that is context sensitive is uAv -> uwv. This is specific because the change of A depends on what’s around it. The cool thing is that this represents english grammar because a word has different meanings in context.
So when trying to figure out if a language is context-free, and you come up with a grammar for it, how do we know you didn’t choose a rule that is context _sensitive_? I guess our rules have to have every item in the left and ride side be different? You can’t do something like aba -> aca but cbc -> cac because that change of the middle b would depend on what is around it.
General grammars are equivalent to turing machines. They both generate context sensitive languages.
Universal turing machine takes an input T, a turing machine. It can simulate T on its own input, x. If this turing machine halts on inputs (T,x) then that means that T halted on x. We need to encode the actual turing machine as a string of symbols.
Universal turing machines are essentially modern computers, as they can execute multiple programs (each of which are their own turing machines).
So in order to encode a turing machine, we pretty much just have to encode its delta function. That is, what state it goes to and what gets read given it’s at a given state, reading a given input. (s,a,q, U) for example.
Encoding input strings is done the same way, and because every string you’ll read is going to be in the language, you just use the encoding that you got from encoding the delta function.
M reads in in encoding of T and encoding of an input to T (x) concatenated… encode(M)encode(x).
What does “recursively enumerable” mean? IT MEANS PARTIALLY DECIDABLE.
The halting problem is: “given a computer program and some input, determine whether or not the program halts/finishes executing”. That is, can a universal turing machine be constructed so that inputs are decidable? Yeah I think that’s what it says. So essentially there is no program you can write that will be able to take any algorithm and an input and decide if that algorithm halts on that input.
Delta is all turing machines that loop on the input of themselves?
Regular languages == regular grammars == deterministic finite automata
Context-free languages == context-free grammars == push down automata
Context-sensitive languages == context-sensitive grammars == linear bounded automata
Recursive languages == (no equivalent grammar) == Turing machines that always halt
Recursively enumerable == general grammars == turing machines
Helpful:
 We now generalize the above reasoning to give a general method for showing
that problems are undecidable. The idea is this: Given that one language
L1 is undecidable, to show that another language L2 is undecidable, give a
procedure to decide L1 given a way to decide L2. Because L1 is undecidable,
there can be no such way to decide L2. Therefore L2 is undecidable also.
We now generalize the above reasoning to give a general method for showing
that problems are undecidable. The idea is this: Given that one language
L1 is undecidable, to show that another language L2 is undecidable, give a
procedure to decide L1 given a way to decide L2. Because L1 is undecidable,
there can be no such way to decide L2. Therefore L2 is undecidable also.
Hierarchy between languages (subsets): Finite < Regular < Context Free < Decidable < Partially Decidable Chomsky normal form: a given transition (e.g. A->BC) must at most result in two non-terminals. So you can’t have A->BCD. Unpacking string n takes 2n-1 steps in this form. PDA determinism: given any config, you can only go to one other config. Turing machine: decidable if halts on all inputs (accepting those in L and rejecting those not), partially decidable if halts on accepted inputs and either halts or loops on rejected inputs. Output is what’s left on the tap after halting. Equivalent to general grammars. General grammar equiv. to context sensitive. They mean that a transition for a character may depend on what’s around it. uAv -> uwv (u, v, don’t change but A going to w requires those surrounding characters). Universal Turing Machine: this is a turing machine that can simulate other turing machines (essentially, a modern computer that can run multiple programs). It takes two inputs, T and x and it runs T on x. If it halts, that means T halted on x. In order to pass a turing machine to a Universal Turing Machine, we have to encode the turing machine being passed. We can do that by encoding its delta function. This is the entire ((q00, a000, q10, a000), (q00, a001, q01, a011)…) business. You encode the input string using the same scheme that you used for the Turing Machine because each character in the language should be defined as an input in the Turing Machine. Passing to a Universal Turing Machine is essentially just concatenating the two encodings: encode(M)encode(x) where M is the Turing Machine and x is the input. Halting Problem is: can you construct a Universal Turing Machine that halts on all inputs, that is, can you create a Universal Turing Machine that is decidable, that is, that can figure out if any algorithm will loop forever. The conclusion is no you can’t create such a Universal Turing Machine.
QUICK AND DIRTY FACTS: Regular are closed under: L1 U L2 (union), L1L2 (concatenation), L1* (kleene star), L1 intersect L2 (intersection). Context free is closed under: union, concatenation, klene star, union with regular, intersection with regular. Iff has finitely many equivalence classes, then L is a regular language. Equivalence with respect to language: for each char in L, next to it what you can add to the end of it (as a set) and still get something into L. Then read off what’s equivalent. Things Turing Machines can recognize (therefore, things that have a General grammar): a^n b^n c^n. Remember, turing machines have a state at any given input as well. We can write this as:
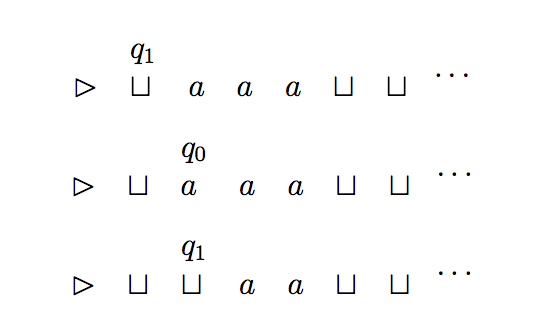
Next: UNDERSTAND THE GENERAL METHOD TO SHOW UNDECIDABILITY. (http://www.cs.unc.edu/~plaisted/comp455/slides/unsolv5.4.pdf) Pumping Lemma: This is to say: If you can choose a string in L of arbitrary length (any n choice) such that if you were to split it up and copy the middle portion a certain number of times, the resulting string would NOT be in L, then you have won and shown that the language is not regular. If the opponent wins, that doesn’t necessarily mean the language is regular. You can’t use the game to show regularity, just show irregularity. Stuff after midterm 2: Chomsky normal form (changing the unpacking steps so that there are most one nonterminal to two nonterminals essentially), which is good because then if you’re doing an exhaustive attempt to generate a string each unpacking for string length n takes 2n-1 steps. Determinism in push down automata, is exactly what you’d expect. At any given configuration, is there more than one transition that you can take to get to the next one? If there isn’t, then it’s deterministic. Context free languages are closed under complementation.
Turing machine can recognize a^nb^nc^n Turing machine is decidable if for all inputs, it accepts those in L and rejects those not in L. So either way it halts. Turing machine semidecides language sigma* if it accepts all inputs in L and rejects or loops all inputs not in L. So accept is always halt but reject may not always be halt. So all machines that are decidable are also semidecidable/partially decidable. So turing machines can accept or reject inputs (both of which are instances of it halting) or it can just loop infinitely.
So to determine the decidability of a problem, we’re actually making a language that represents that problem and then seeing if there’s a turing machine that accepts that language. Output of a turing machine is what’s left on the tap after halting. Busy beaver function essentially shows that some machines will halt after a large number of steps and so you can’t say “let’s just compute first 1000 iterations and if it doesn’t halt then it’ll never halt” because some might. One thing to know is that nondeterminism doesn’t add power, but I don’t really understand what it is. It seems like you have have multiple transitions for a given configuration and your automaton essentially (you can imagine it like this) takes all transitions possible and then it would have guessed the right one. General grammars are more reaching and they encompass I think any of the grammars we’ve talked about. For example, context free grammars are also general grammars. Context sensitive/specific is interesting. An example of a production that is context sensitive is uAv -> uwv. This is specific because the change of A depends on what’s around it. The cool thing is that this represents english grammar because a word has different meanings in context. So when trying to figure out if a language is context-free, and you come up with a grammar for it, how do we know you didn’t choose a rule that is context _sensitive_? I guess our rules have to have every item in the left and ride side be different? You can’t do something like aba -> aca but cbc -> cac because that change of the middle b would depend on what is around it. General grammars are equivalent to turing machines. They both generate context sensitive languages. Universal turing machine takes an input T, a turing machine. It can simulate T on its own input, x. If this turing machine halts on inputs (T,x) then that means that T halted on x. We need to encode the actual turing machine as a string of symbols. Universal turing machines are essentially modern computers, as they can execute multiple programs (each of which are their own turing machines). So in order to encode a turing machine, we pretty much just have to encode its delta function. That is, what state it goes to and what gets read given it’s at a given state, reading a given input. (s,a,q, U) for example. Encoding input strings is done the same way, and because every string you’ll read is going to be in the language, you just use the encoding that you got from encoding the delta function. M reads in in encoding of T and encoding of an input to T (x) concatenated… encode(M)encode(x). What does “recursively enumerable” mean? IT MEANS PARTIALLY DECIDABLE. The halting problem is: “given a computer program and some input, determine whether or not the program halts/finishes executing”. That is, can a universal turing machine be constructed so that inputs are decidable? Yeah I think that’s what it says. So essentially there is no program you can write that will be able to take any algorithm and an input and decide if that algorithm halts on that input. Delta is all turing machines that loop on the input of themselves? Regular languages == regular grammars == deterministic finite automata Context-free languages == context-free grammars == push down automata Context-sensitive languages == context-sensitive grammars == linear bounded automata Recursive languages == (no equivalent grammar) == Turing machines that always halt Recursively enumerable == general grammars == turing machines Helpful:
We now generalize the above reasoning to give a general method for showing that problems are undecidable. The idea is this: Given that one language L1 is undecidable, to show that another language L2 is undecidable, give a procedure to decide L1 given a way to decide L2. Because L1 is undecidable, there can be no such way to decide L2. Therefore L2 is undecidable also.