An exploration of a question regarding a beam of light from a flashlight being obstructed by a piece of paper. I believe Tara and I worked on this problem together.
read moreIf I'm holding a flashlight with a small rectangular piece of paper obstructing the beam of light thus creating a shadow, what's an equation that defines the area of the shadow as a function of the dimensions of the paper and its distance from the flashlight? It's obviously inversely proportional to the distance, but is it "to the distance squared"? Something else?
If the piece of paper was very small compared to the size of the flashlight/radius of the cone, then the area of the shadow wouldn’t change that much depending on the distance from the flashlight.
Wouldn’t this be the case only if the origin of the light were not a point source? Because it seems to me that no matter what the size of the piece of paper, it could be moved so close to the light source that the shadow grew very large as almost all the light was blocked.
Also note that it seems like you could put the shadow on a gradient whose endpoints are the actual size of the card and a shadow infinitely large (the light source is completely blocked). We must also consider the distance between the card and the surface the shadow is casted upon. When the card is placed on the surface the shadow is projected on, the shadow has reached its minimum (the size of the card). When the card is placed on the light source, it has reached is maximum (infinite/undefined).
A = area of shadow
a = area of paper
d = degrees up and down from 0 degrees
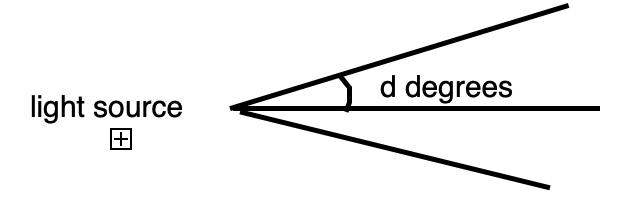
A = a/d (need some coefficient for the angle of the cone of light...the greater the angle, the more the shadow changes as d changes)
A = a/(d*degrees) ???
if a is sufficiently small, then d doesn’t affect it. If the angle is like 0 degrees then that is the same as a being sufficiently small.
If you were to define the cone of light algebraically, could you solve this with no knowledge of optics? Does a knowledge of optics even help at all with this question?
Maybe knowledge of optics helps determine when you should treat the flashlight more like a cone of light (and how to define this algebraically) and when it should be treated as so much larger that...or maybe not. hohohm
What is it about the generation of light that makes it propagate in every direction (this goes back on my original question also on the generation of visible light)?