An in-depth intuitive look at this fundamental principle in Calculus. This was fascinating math.
read moreRight, left, or midpoint Riemann sum doesn’t really matter so claimed because it’s being multiplied by a very small number (delta x). But, if you consistently make an error (you’re taking the left sum of a function that’s concave up, then you should still get the error). My question is what happens to this error if it’s an improper integral (such 0 to infinity)?
All right, revisiting this, we can say that the midpoint on a very small interval can be considered the constant that you multiply delta x by.
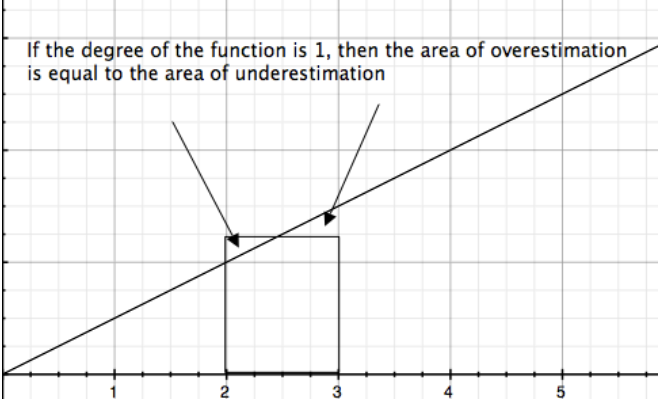
This is do to the fact that the concavity is zero (degree of the function is less than or equal to 1).
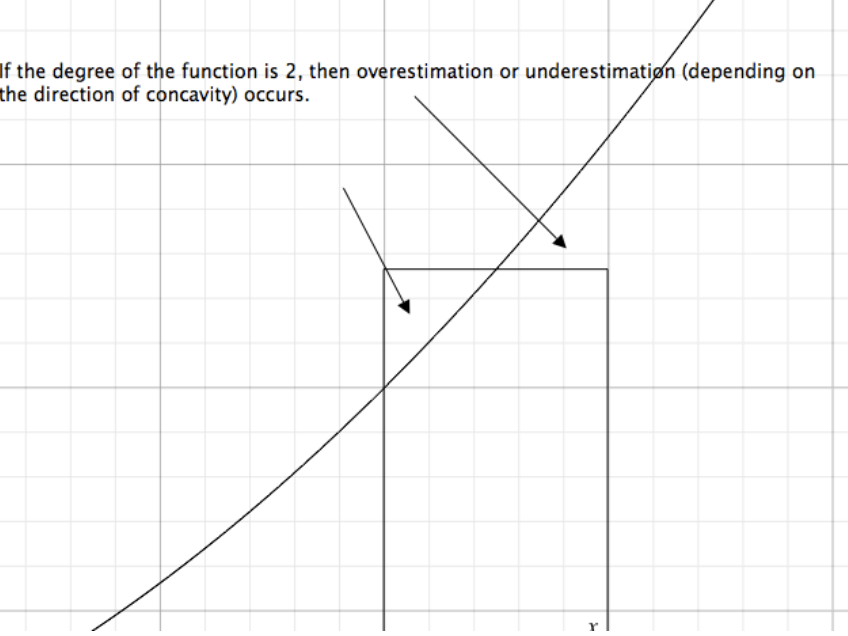
Now, what I’d like to think about is taking into account the concavity. Adding a constant of concavity (or subtracting depending on the direction of concavity) from the midpoint taken would allow for a more accurate integral.
For taking a Riemann sum, why don’t we factor in the first derivative to reduce error?
For the object with a base of a circle with square cross sections, you have the rate of the increase of the base (the circular base) should be equal to the rate of the increase of the top which is a dome. This is because it’s a square. So, it’s saying that the curvature is of the base is equal to the curvature of the top of the dome. That’s interesting.
Now, if you were to have a base that was a circle and rectangular cross sections with a constant height, you would be getting sector of a cylinder.
Would you use a double integral to calculate the area of a torus?
If you bring a line through a line you get a plane. If you bring an area through a line you get an object. If you bring a line through a point you get a line. If you bring a plane through a plane...I think you get a four dimensional object. To bring one thing through another is to multiply to two.
The dimensionality is dependent upon the highest degree of what you bring through what. i.e.
3d = x^3
Plane = x^2
Line = x^1
Point = x^0
To put what is stated above mathematically: x^1 * x^1 = x^(1+1) or x^2, hence plane.