An examination of the square roots of numbers and their midpoints.
read moreLook at the tendency of a square root to lean to either of the two nearest squares as a function of the size of the number.
sqrt(27) is between 5 and 6, how does this square root lean to 5 or 6. If we move to a number between 7 and 8, how does this change?
Let’s look at the halfway point between some squares:
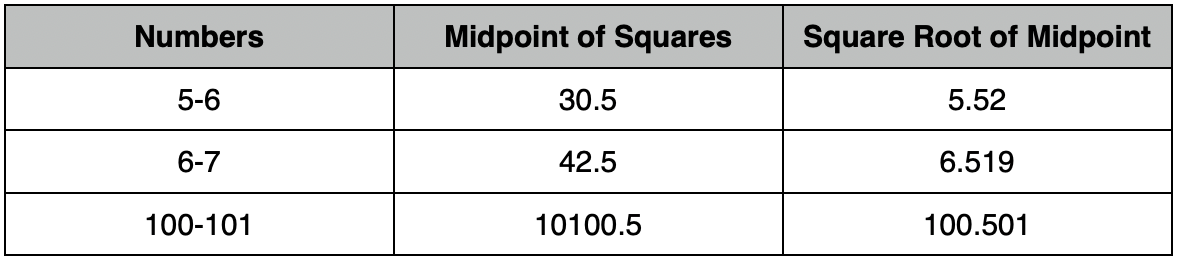
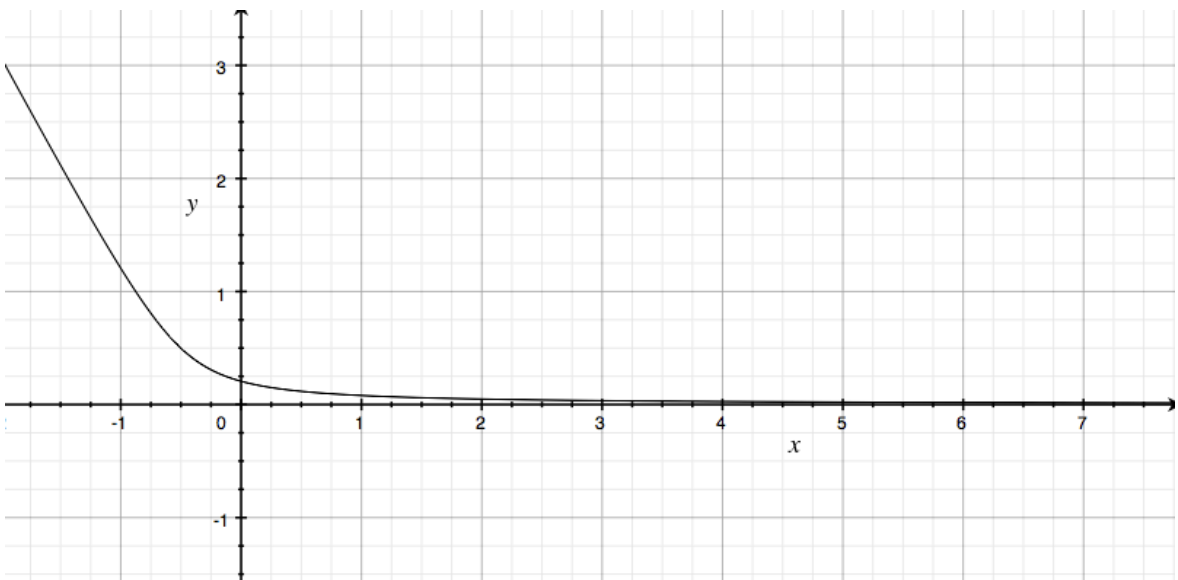
So it just appears as though we are getting closer to the midpoint between the two numbers as the numbers get larger. Below is a graph of the difference between the square root of the midpoint and the midpoint of the two numbers. sqrt((x^2 + (x+1)^2)/2) - (2x+1)/2