An examination of how quickly a function will diverge/converge.

read more

We now think of the rate of change of the integral.

We have some function that may or may not diverge when integrated entirely (on the interval negative to positive infinity).

What we want to find is the rate at which it approaches infinity so that we may compare it with other functions.

Now, this may seem difficult, but it may be as easy as:

Given: 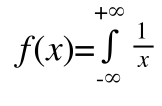(change from 1 to infinity)

Distance would be something like 0 - f(x)

But, now we have to kind of think of the rate of change of the integral. That would just be the original function.

But, we want to see how quickly the functions integral approaches infinity. Now, we’d do this by finding the rate of change of the integral, which would be the original function...Hm, interesting. So somehow, the rate at which f(x) approaches infinity is 1/x. So, its rate is changing. Maybe we could do something with finding the average rate of change. That would be by dividing the functions integral by the interval. That’d be impossible because the function diverges. Maybe we could do it for converging functions. I’ll have to think about this more later, my computer is about to die.

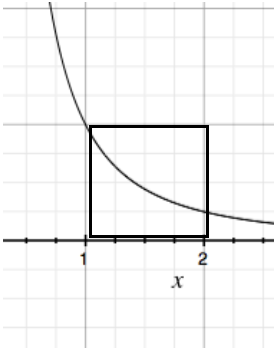
All right, revisiting and thinking about the integral of 1/x^2 from 1 to infinity means that the entire area is going to be equal to or at least approaching the 1 by 1 block [1,2],[1,0],[2,0],[2,1] (it’s interesting how the corners of the box are permuting…

The entire area fills in the box, it’s imagine the line coiling within the box.