I became obsessed with dynamical systems in 10th grade, and studied them at Summer Ventures of Science and Math.
A dynamical system is, at its core, a system that uses the output of the prior run of the function as the new input. Clearly, then, its importance cannot be understated: the universe is a dynamical system. We simply take the state of the world at one timeslice, apply all of the laws of physics to it, and we can with certainty compute the next timeslice. The future is simply the present with the laws of physics played out a little bit farther. At least, that's how us determinists see the world.
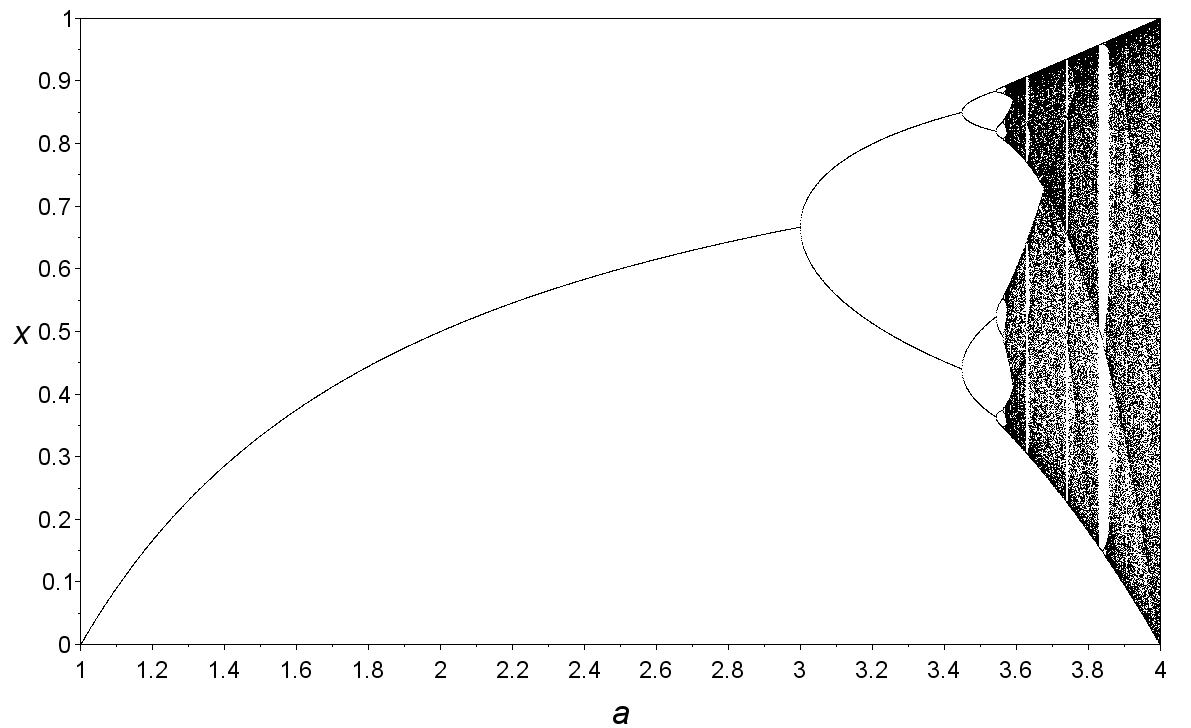
read moreA very simple dynamical system is k * (x - (x^2)) where we choose some value for k and x and then take the output of the function and plug that output in as x for the second run, and repeat that process infinitely. Often, something very simple happens: the outputs settle down on a single value. But here's where things get incredibly interesting (this is probably the most interesting thing I've encountered in mathematics). As you increase the value of k, from say 2 to 3.2, and all of a sudden instead of settling down on a single value, the system doesn't settle down to one value. Instead, it bounces between two values. Forever. Increase k a bit more? All of a sudden it starts to bounce between four values instead of two (this is called period doubling). Then 8. Then 16. And then all of a sudden something remarkable happens: it stops settling down at all. It becomes chaotic. Complete and utter chaos. Then as you raise k a bit more and more, calm in the middle of the storm: it starts to settle down on a couple of values again. Increase it more? Back to chaos. This phenomenon is not isolated to this equation. It's seen everywhere.
I created a small program in Mathematica that allows you to manually change k (and the starting value of x, which is much less consequential) to demonstrate this effect (it's difficult to understand but reflecting the input off the x=y line is the same as plugging in the prior output as the new input. You can see that as k increases, the value after 30 iterations goes from converging on a single value, to instead bouncing back and forth between two values. Then, eventually, it doesn't settle down at all.
This phenomenon is captured on something called a bifurcation diagram (called that because the period, that is the value that the system settles down on, bifurcates, i.e. splits in two, as k increases, until it becomes chaotic). Bifurcation diagrams remain one of the most simultaneously beautiful and eerie plots I've seen in math.
Manipulate[
Show[ListLinePlot[
Flatten[
Table[{Nest[Function[x, k*(x - (x^2))], startingValue, i + j - 1],
Nest[Function[x, k*(x - (x^2))], startingValue, i]}, {i, 1,
30}, {j, 0, 1}], 1], PlotRange -> {{0, 1}, {0, 1}},
Epilog -> {Arrowheads[.02], Hue[0.67, 0.6, 0.6],
Arrow[{{startingValue, 0}, {startingValue,
k*(startingValue - startingValue^2)}}]}],
Plot[k*(x - x^2), {x, 0, 1}, PlotLabel -> "k(x-x^2)"],
Plot[x, {x, 0, 1}]], {{startingValue, 0, "Initial Value"}, 0, 1,
Appearance -> "Labeled"}, {{k, 1, "k value"}, 1, 4,
Appearance -> "Labeled"}]
Dynamical System Demonstration
Bifurcation Diagram